Due to permanent lack of time and really long personal TODO list I’m not frequent crackme-solver, but sometimes it is good to check if my skills didn’t get rusty. I’ve browsed through unsolved crackmes on crackmes.de and found quite new gim913’s crackme that was unsolved for almost 2 months (yup, I know that it’s not much :) ). Knowing reputation of the author I’ve decided to give it a try, as probably there will be something interesting inside. So, let’s start.

Static analysis

Crackme is written in pure C++ without any obfuscation and anti-debugging, loading it to some old version of IDA didn’t showed much. Crackme was compiled by Visual Studio 2010, so I had to update my IDA signatures. Quick PEiD scan revealed that crackme is using MD5 algorithm, which is worth to note, because I’ll take advantage of this info later. Identifying function that is responsible for user/pass check is fairly easy, looking for references to below strings may help:

.rdata:0041C560 db 'C O N G R A T U L A T I O N S !',0
.rdata:0041C580 db 'Wrong username!',0
.rdata:0041C590 db 'Wrong password!',0

All those strings are referenced by function that starts at 0x0040188E address and this function plays a main role in the crackme, so I’ll call it serial_check() and refer to it by that name. serial_check() is quite long (almost 3kB of binary code) and calls many unrecognized functions. Manual analysis of those calls could take some time, but there is an easier way. I’ve looked at constant strings embedded in the executable and after filtering out all common strings that are in every executable, I’ve found some suspicious strings:

.rdata:004191AC db '3.90625E-3',0
.rdata:004191B8 db '1.5625E-2',0
.rdata:004191C4 db '8.0E-3',0
.rdata:004191CC db '0.85',0
.rdata:004191D4 db '0.5',0
.rdata:004191D8 db '10',0

Querying google for the first two values reveal many results, but most of them are irrelevant. I’ve found what I was looking for at 9th and 10th place on the first page, it was part of the source code of MAPM Library:

    m_apm_set_string(MM_5x_125R, "8.0E-3");
    m_apm_set_string(MM_5x_64R, "1.5625E-2");
    m_apm_set_string(MM_5x_256R, "3.90625E-3");

MAPM, A Portable Arbitrary Precision Math Library in C is quite old (and previously unknown to me), complex library for various math computations, it supports big integers as well as big floating point values. I’ve managed to compile MAPM with Visual Studio 2010 (library has batch script for VC 6.0 and it still works). IDA signatures made from that lib were partially ok, IDA matched 23 out of ~40 functions. Not matched functions were easily recognizable manually, by matching source code with overall structure of each not recognized function and by looking at references to other recognized functions and data.

Besides low-level api for numerical computations, MAPM library has also wrapper class that implements all operators, so it can be used almost transparently. Mentioned wrapper isn’t included in the library itself, it is part of the header file, so I had to manually resolve also functions from this class. After this initial analysis serial_check() looks a bit more friendly, but there was still a lot of unrecognized functions. It is because of heavy usage of STL, if I’m correct, crackme uses std::string, std::vector and std::list to maintain MAPM structures during execution. I’ve decided to not bother with exact recognition of all those functions, because all in all I didn’t need it. That’s pretty much all of static analysis.

Dynamic approach

For easier debugging I’ve removed ASLR from the executable. First of all I’ve checked which data are hashed by MD5, triggering breakpoint on MD5 function showed that MD5 is calculated from username, so I had first step for keygen:

    usermd5 = MD5(username);

Second guess (my dynamic approach was ‘guessing game’ until I’ve reached point, where I was sure what is what) was related to MAPM library, it is using m_apm_set_long() function to initialize MAPM object with integer value:

void m_apm_set_long(M_APM, long);

I’ve set breakpoint on that function and just waited, it was good guess, I’ve logged values that were going to this function:

 0x00, 0x67, 0x100, 0x69, 0x100, 0x6D, 0x100, 0x39, 
        'g'          'i'          'm'          '9'
 
0x100, 0x31, 0x100, 0x33, 0x100, 0x21, 0x100, 0x95
        '1'          '3'          '!'

I’ve traced function that is calling m_apm_set_long() with above values, and I was able to deduce that it is creating some bignum value from given string:

MAPM createValue(unsigned char* data, unsigned int dataSize)
{
	MAPM v = 0;
	for (unsigned int i = 0; i < dataSize; i++)
	{
		v *= 0x100;
		v += data[i];
	}
	return v;
}

String “gim913!\x95” is evaluated to 7451607150867194261, which is prime value. This is second information that will be used in keygen:

    MAPM p = createValue("gim913!\x95");

Further logging of m_apm_set_long() revealed that MD5 from username is used to initialize 4 values, so next steps for keygen:

    MAPM a = createValue(usermd5, 5);
    MAPM b = createValue(usermd5 + 5, 5);
    MAPM c = createValue(usermd5 + 10, 5);
    MAPM d = createValue(usermd5 + 15, 1);

At this point I could switch back to serial_check() function, as most of calculations is done there by various MAPM functions. When username is preprocessed, crackme adjusts ‘b’ value:

    b = (512 * b) + d;

Then it calculates:

    MAPM D = b*b - 4*a*c;

Above formula is nothing more than discriminant of the quadratic equation and in this case it is used to check if crackme is keygenable for given username. Crackme at first checks if D >= 0, if it is it performs additional calculations:

    D %= p;
    MAPM A = powmod(D, (p - 1)/2, p);

Above formula is called Legendre symbol and it is used to check if value is quadratic residue modulo prime number. If it isn’t, crackme will generate “Wrong username!” message. Some of you probably already know what was the protection scheme but I’ll quote Steve Jobs:

“… you can’t connect the dots looking forward; you can only connect them looking backwards. So you have to trust that the dots will somehow connect in your future.”

So, I didn’t connected the dots, because my knowledge about quadratic congruence equations was equal to zero. Let’s leave it for now, I was performing further analysis of serial_check() function. Next part of serial_check() was filled with bunch of calls to unrecognized functions that were forming loop. That wasn’t encouraging, so I’ve decided to do some wild guess and I’ve set hardware breakpoint on memory where inscribed serial number was stored. After first hit I’ve traced values that were taken from serial number, few functions above I saw that each character from serial number is converted to int value, but not all characters, only numbers and big letters (at least A-F, because I was trying hex numbers as a serial number). Each value was then processed by below algorithm:

int V = 0;
for (int i = 0; i < cnt; i++)
{
	V *= 36;
	V += getNextValueFromSerialNumber();
}

Identification was rather easy, it is base36 converter. It is called 3 times, each time converts 5 letters from serial number to int value, so proper serial number should be 15 characters long composed from below charset:

"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"


Values gathered from serial number will be called sn1, sn2, sn3. Each sn value is checked by below algorithm:

    unsigned int v;  // word value to compute the parity of
    v ^= v >> 16;
    v ^= v >> 8;
    v ^= v >> 4;
    v &= 0xf;
    return (0x6996 >> v) & 1;

It is checking if v contains odd or even number of bits set, crackme requires even numbers. After this check, sn values are shifted by one in the right direction:

    sn1 >>= 1;
    sn2 >>= 1;
    sn3 >>= 1;
    sn1 &= 0xFFFFFF;
    sn2 &= 0xFFFFFF;
    sn3 &= 0xFFFFFF;

Thanks to this operation, parity check doesn’t interfere with values that will be used in equation. SN values are used then to create one value:

    MAPM SN = (sn1*0x1000000 + sn2)*0x1000000 + sn3;

How do I know? Again, old breakpoint that was set on m_apm_set_long() at the beginning of this paragraph comes in handy. The last step performed by serial_check() function is calculation of value described by below formula and comparing it to 0:

    MAPM Y = (a*SN*SN + b*SN + c) % p;

Quadratic Congruence Equation

Solving this equation is fairly simple, but due to lack of proper knowledge I was struggling on it for some time. I asked for help my old friend from http://gdtr.wordpress.com/ and he pointed out some resources that I should read before solving it. At first I’ve tried WolframAlfa to check if everything is correct, so I’ve wrote down my equation with coefficients generated from username “ReWolf” and I’ve received below results:

Then I’ve converted roots to proper base36 serial number and crackme showed “C O N G R A T U L A T I O N S !” message box. Now how to solve it manually ? Basically the solution is similar to standard quadratic equation, but all operations should take into account modular arithmetic.

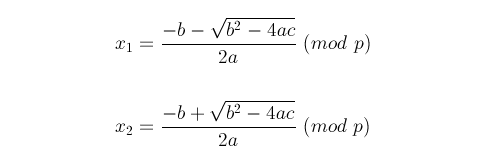
There are two problems in the above formulas:

• modular multiplicative inverse
• modular square root

First problem can be solved by extended Euclidean algorithm, second is more complicated but there are few algorithms that can help:

• Tonelli-Shanks algorithm
• Cipolla’s algorithm
• Pocklington’s algorithm

I’ve chosen Tonelli-Shanks as it seems to be most popular solution, at least from the google search perspective. In the keygen I’ve used Tonelli-Shanks implementation written by Eli Bendersky:

http://eli.thegreenplace.net/2009/03/07/computing-modular-square-roots-in-python/

It’s written in python, but it was very straightforward to port it to C++. That’s pretty much all, check source code of a keygen for implementation details.

Erratum

Here are a few post-analysis details that I’ve learned from the crackme author after I’ve sent him keygen:

• MD5 is taken from Crypto++ Library
• Crackme is really using STL: <map>, <list>, <string>, <vector>, <algorithm>
• Crackme is using FC++: Functional Programming in C++ to “obfuscate” code
• Those few strings that I’ve used to identify MAPM Library were left intentionally as a hint for cracker

Author was kind enough to send me source code of the crackme, here are my favourite fragments:

• Creating MAPM object from std::string:

std::string gim913 = "\x67\x69\x6d\x39\x31\x33\x21\x95"; MAPM prime = foldl([](MAPM left, int b) { return 256*left + b; }, mapm_zero, List<e_ubyte>(gim913.begin(), gim913.end()));

std::string gim913 = "\x67\x69\x6d\x39\x31\x33\x21\x95"; MAPM prime = foldl([](MAPM left, int b) { return 256*left + b; }, mapm_zero, List<e_ubyte>(gim913.begin(), gim913.end()));

• Parsing MD5:

auto res = splitAt(5, chunks_mdu); coefficients.push_back( foldl([](MAPM left, int b) { return 256*left + b; }, mapm_zero, res.first) );

auto res = splitAt(5, chunks_mdu); coefficients.push_back( foldl([](MAPM left, int b) { return 256*left + b; }, mapm_zero, res.first) );

References (other than already mentioned)

• http://math.stackexchange.com/questions/160385/how-to-solve-this-quadratic-congruence-equation
• http://math.stackexchange.com/questions/30778/is-there-a-formula-for-solving-the-congruence-equation-ax2-bx-c-0
• http://en.wikipedia.org/wiki/Extended_Euclidean_algorithm
• http://www.johndcook.com/quadratic_congruences.html
• http://www.alpertron.com.ar/QUADMOD.HTM